Решение логических задач
Как решать логические задачи?
Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:
- средствами алгебры логики;
- табличный;
- с помощью рассуждений.
I. Решение логических задач средствами алгебры логики.
Обычно используется следующая схема решения:
1. изучается условие задачи;
2. вводится система обозначений для логических высказываний;
3. конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
4. определяются значения истинности этой логической формулы;
5. из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Пример.
Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение.
Введем обозначения для логических высказываний:
Ш — победит Шумахер;
Х — победит Хилл;
А — победит Алези.
Реплика Ника "Алези пилотирует самую мощную машину" не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
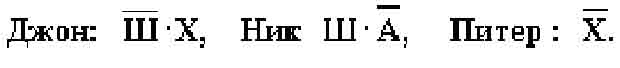
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
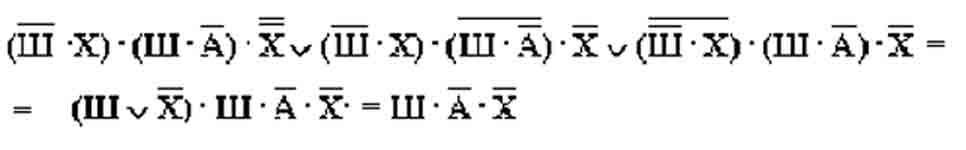
Высказывание истинно только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
II. Решение логических задач табличным способом.
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.
Пример. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Браун любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение.
Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
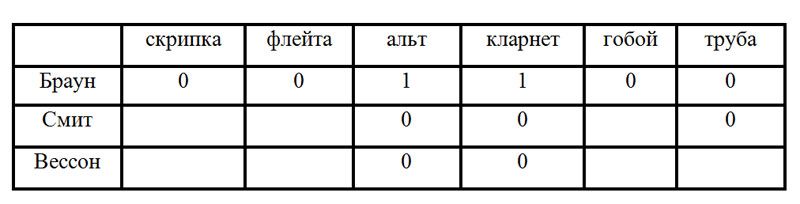
Так как музыкантов трoе, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют.
Из условия 4 следует, что Смит не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна — альт и кларнет. Занесем это в таблицу, а оставшиеся клетки столбцов "альт" и "кларнет" заполним нулями:
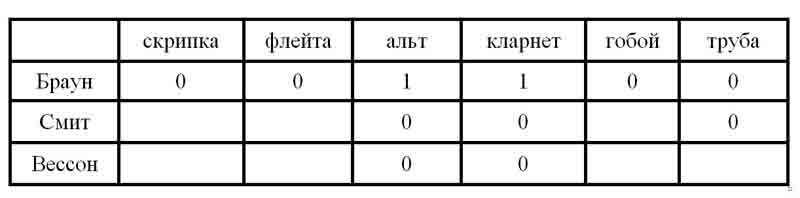
Из таблицы видно, что на трубе может играть только Вессон.
Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки "Вессон" можно заполнить нулями:
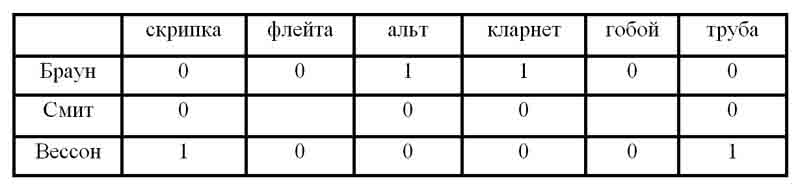
Из таблицы видно, что играть на флейте и на гобое может только Смит.
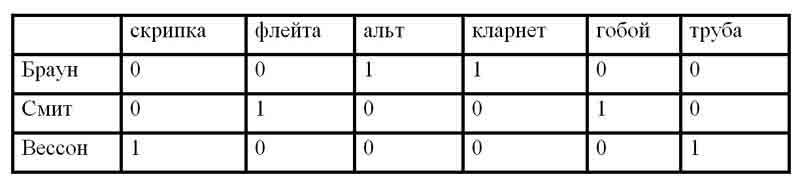
Ответ. Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе.
Пример.
Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Решение. Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
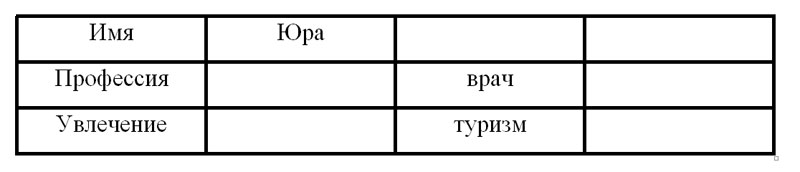
Буква "а", присутствующая в слове "врач", указывает на то, что Влад тоже не врач, следовательно врач — Тимур. В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра. Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем:

Ответ. Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
III. Решение логических задач с помощью рассуждений.
Этим способом обычно решают несложные логические задачи.
Пример.
Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение. Имеется три утверждения:
1. Вадим изучает китайский;
2. Сергей не изучает китайский;
3. Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ. Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Задачник
-
Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда, тоже очень талантливы. Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго.
Известно, что:
- Джуди живет не в Париже, а Линда — не в Риме;
- парижанка не снимается в кино;
- та, кто живет в Риме, певица;
- Линда равнодушна к балету.
Где живет Айрис, и какова ее профессия?
- Пытаясь вспомнить победителей прошлогоднего турнира, пять бывших зрителей турнира заявили:
- Антон был вторым, а Борис - пятым.
- Виктор был вторым, а Денис - третьим.
- Григорий был первый, а Борис - третьим.
- Антон был третьим, а Евгений - шестым.
- Виктор был третьим, а Евгений - четвертым.
Впоследствии выяснилось, что каждый зритель ошиб¬ся в одном из двух своих высказываний. Каково было истинное распределение мест в турнире?
-
В школе, перешедшей на самообслуживание, четырем старшеклассникам: Андрееву, Костину, Савельеву и Давыдову поручили убрать 7-ой, 8-ой, 9-ый и 10-ый классы. При проверке оказалось, что 10-ый класс убран плохо. Не ушедшие домой ученики сообщили о следующем:
- Андреев: «Я убирал 9-ый класс, а Савельев — 7-ой».
- Костин: «Я убирал 9-ый класс, а Андреев — 8-ой».
- Савельев: «Я убирал 8-ой класс, а Костин - 10-ый».
Давыдов уже ушел домой. В дальнейшем выяснилось, что каждый ученик в одном из двух высказываний говорил правду, а во втором ложь. Какой класс убирал каждый ученик?
-
Пять школьников из пяти различных городов Брянской области прибыли для участия в областной олимпиаде по математике. На вопрос: «Откуда Вы?» каждый дал ответ:
- Иванов: «Я приехал из Клянцов, а Дмитриев из Новозыбкова».
- Сидоров: «Я приехал из Клянцов, а Петров из Трубчевска».
- Петров: «Я приехал из Клянцов ,а Дмитриев из Дятькова».
- Дмитриев: « Я приехал из Новозыбкова, а Ефимов из Жуковки».
- Ефимов: « «Я приехал из Жуковки, а Иванов из живет в Дятькове».
Откуда приехал каждый из школьников, если одно его утверждение верно, а другое ложно?
-
На соревнованиях по легкой атлетике Андрей, Борис, Сергей и Володя заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись.
- Даша сказала: "Андрей был первым, а Володя - вторым".
- Галя утверждала: "Андрей был вторым, а Борис - третьим".
- Лена считала: "Борис был четвертым, а Сергей - вторым".
Ася, которая была судьей на этих соревнованиях и хорошо помнила, как распределились места, сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление.
Кто из мальчиков какое место занял?
-
Кто из друзей (Иван, Петр, Алексей, Николай или Борис) коллекционирует марки, если известно, что:
- если Борис коллекционирует марки, то их коллекционируют Иван и Николай;
- если их коллекционирует Иван, то Петр тоже коллекционирует марки;
- из двух друзей (Петра и Алексея) коллекционирует марки только один;
- Алексей лишь в том случае коллекционирует марки, если их коллекционирует Николай;
- по крайней мере, Николай или Борис коллекционирует марки.
-
На вопрос, кто из трех абитуриентов A, B, C может работать на компьютере, был получен ответ: если может работать B, то может работать и C, но не верно, что если может работать A, то может работать и C. Кто из трех абитуриентов может работать на персональном компьютере?
-
На вопрос, какая завтра погода, синоптик ответил: если не будет ветра, то будет пасмурная погода без дождя; если будет дождь, то будет пасмурно и без ветра; если будет пасмурно, то будет дождь и не будет ветра. Подумав немного, синоптик уточнил, что его три высказывания можно записать более лаконично. Попробуйте это сделать!
-
На олимпиаде по информатике студенты A, B, C и D заняли первые четыре места. Когда их спросили о распределении мест, они дали три ответа: D – первый или B – второй; C – первый или A – четвертый; D – второй или B – третий. Как распределились места, если в каждом ответе только одно утверждение истинно?
-
Кто из абитуриентов A, B, C и D играет, а кто не играет в шахматы, если известно следующее: если A или B играет, то C не играет; если B не играет, то играют C и B; C – играет. Решить задачу с помощью логических операций.
-
В деле об убийстве имеются двое подозреваемых: A и B. Допросили четверых свидетелей. Показания первого таковы: «A не виноват». Второй свидетель сказал: «B не виноват». Третий свидетель: «Из двух показаний по крайней мере одно истинно». Четвертый: «Показания третьего свидетеля ложны». Четвертый свидетель оказался прав. Кто же совершил преступление?
-
Аня, Вика и Сергей решили пойти в кино. Учитель хорошо знавший этих ребят, высказал следующие предположения: Аня пойдет в кино только тогда, когда пойдут Вика и Сергей; Аня и Сергей пойдут в кино вместе или же оба останутся дома; чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика. Когда ребята пошли в кино, оказалось, что учитель немного ошибался, из трех его утверждений истинными оказались только два. Кто из названных ребят пошел в кино?
-
Костя пригласил свою сестру приехать к нему в гости. После этого он получил от нее три сообщения: я приеду в гости, если только со мной приедет папа; чтобы я приехала, необходимо, чтобы меня сопровождала мама; либо приедем мы с мамой, либо приедет только папа. Когда приехали гости, оказалось, что из этих трех сообщений истинным было только одно. Кто приехал навестить Костю?
-
Студенты узнали, что к ним в группу должен придти юноша из другого института. Обсуждая эту новость, студенты высказали ряд предположений: для того, чтобы новичок был добрым, достаточно чтобы он был умным; если новичок силач, то он либо глупый, либо злой; если новичок умный, то для того, чтобы он был добрым, необходимо, чтобы он бы сильным. Преподаватель сказал, что из этих условий выполнено только одно. Кроме того, преподаватель сказал: «Необходимое условие доброты – это ум. Значит, новичок умный, но слабый». Каким был новичок?
-
Пятеро друзей.
Пятеро друзей решили записаться в кружок любителей логических задач: Андрей (А), Борис (Б), Виктор (В), Григорий (Г), Дмитрий (Д). Но староста кружка предложил им выдержать вступительный экзамен. «Вы должны приходить к нам по возможности больше вечеров, однако, в разных сочетаниях, соблюдая следующие условия:
а) Если А приходит вместе с Д, то Б должен присутствовать.
б) Если Д отсутствует, то Б должен быть, а В пусть не приходит.
в) А и В не могут одновременно ни присутствовать, ни отсутствовать.
г) Если приедет Д, то Г пусть не приходит.
д) Если Б отсутствует, то Д должен присутствовать, но это в том случае, если не присутствует В. Если же В присутствует при отсутствии Б, то Д приходить не должен, а Г должен прийти.»
Сколько вечеров и в каком составе друзья могли прийти?
-
Обед с логикой.
N хотел пригласить на обед по возможности больше соседей: A, B, C, D, E, F, G, H. При этом он столкнулся со следующими трудностями:
1) A никогда не придет, если пригласить B или C или если одновременно пригласить D и E.
2) D придет только в том случае, если будет приглашен и E.
3) E не примет только в том случае, если придет B.
4) F наносит визиты только в сопровождении G.
5) H не будет возражать против присутствия F только в том случае, если будет приглашен и A.
6) Если не будет приглашен F, то H будет против приглашения E.
7) Чтобы пришел G, необходимо пригласить D или H.
8) G откажется от приглашения, если пригласят E без A, а также в случае приглашения B или C.
Какое минимальное число гостей и кого именно мог пригласить N?
-
Диагностическая.
Имеются два симптома S1 и S2 двух болезней X1 и X2. Известно:
1) При X2 есть S1.
2) При X1 и отсутствии X2 есть S2.
3) При X2 и отсутствии X1 нет S2.
4) При S1 или S2 есть, по крайней мере, X1 или X2.
Составьте логическое уравнение, позволяющее по «значениям» признаков («есть», «нет») определить «значения» болезней.
-
Экономическая.
Менеджер банка должен установить 4 банкомата. В течение каждого дня работы должны выполняться следующие условия:
1) Если работает первый банкомат, то третий банкомат не должен работать, а второй и четвертый должны.
2) Если работает третий банкомат, то первый и четвертый не должны работать, а второй должен.
3) Должен работать по крайней мере один банкомат.
Необходимо определить наибольшее число дней, которое могут работать банкоматы при выполнении этих условий, так, чтобы их назначение ни в один из дней не повторялось, а также указать допустимое расписание на каждый день.
-
Для полярной экспедиции из восьми претендентов A, B, C, D, E, F, G, H надо отобрать шесть специалистов: биолога, гидролога, синоптика, радиста, механика и врача. Обязанности биолога могут выполнять E и G, гидролога – B и F, синоптика F и G, радиста – C и D, механика C и H, врача A и D. Хотя некоторые претенденты владеют двумя специальностями, в экспедиции сможет выполнять только одну. Кого и кем следует взять в экспедицию, если F не может ехать без B, D – без H и без C, C не может ехать одновременно с G, а A не может ехать вместе с B?
-
Спортивная.
Шесть спортсменов – Адамов, Белов, Ветров, Дронов, Ершов – в проходившем соревновании заняли шесть первых мест, причем ни одно место не было разделено между ними. О том, кто какое место занял, были получены такие высказывания:
1) «Кажется, первым был Адамов, а вторым – Дронов»;
2) «Нет, на первом месте был Ершов, а на втором – Глебов»,
3) «Вот так болельщики! Ведь Глебов был на третьем месте, а Белов – на четвертом»;
4) «И вовсе не так: Белов был пятым, а Адамов – вторым»;
5) «Все вы перепутали: пятым был Дронов, перед ним – Ветров».
Известно, что в высказывании каждого болельщика одно утверждение истинное, а другое ложное. Определите, какое место занял каждый из спортсменов.
- Коробочки
Есть пять коробочек: белая, черная, красная, синяя и зеленая. И десять шариков тех же цветов, что и коробочки, по два каждого цвета. В каждой коробочке лежат по два шарика. При этом:
1) ни один шарик не лежит в коробочке того же цвета, что и он сам;
2) в красной коробочке нет синих шариков;
3) в коробочке нейтрального цвета (белый или черный) лежат один красный и один зеленый шарик;
4) в черной коробочке лежат шарики холодных тонов (зеленые и синие тона);
5) в одной из коробочек лежат один белый и один синий шарик;
6) в синей коробочке находится один черный шарик.
Какого цвета шарики лежат в какой коробочке?
-
На десяти карточках написано по одному целому числу от 1 до 10. Пятеро людей вытягивали по две карточки и называли сумму чисел. В итоге известно, что получились следующие суммы:
1) 1 - 11,
2) 2 – 4;
3) 3 – 7;
4) 4 – 16;
5) 5 – 17.
Установить какие числа выпали каждому?
-
Среди гостей присутствуют пять офицеров: пехотинец, артиллерист, летчик, связист и сапер. Один из них – капитан, трое – майоры и один – подполковник. Известно, что:
1) у Яноша такое же звание, как и у его друга сапера;
2) офицер-связист и Ференц – большие друзья;
3) офицер-летчик вместе с Белой и Лайошем недавно побывали в гостях у Ференца;
4) незадолго да званного вечера у артиллериста и сапера почти одновременно вышли из строя радиоприемники. Оба в один день обратились к Лайошу с просьбой зайти к ним и помочь связисту установить неисправность и не ошиблись, поскольку с тех пор приемники у обоих работают отлично;
5) Ференц чуть было не стал летчиком, но потом по совету своего друга сапера избрал иной род войск;
6) Янош по званию старше Лайоша, а Бела старше Ференца;
7) пятый офицер, Андраш, накануне вечера был в гостях у Лайоша.
Определите звание каждого офицера и род войск, в котором он служит.
-
В библиотеке не хватает пяти книг:
- томика Жюля Верна;
- романа Чарлза Диккенса;
- сборника рассказов Жигмунда Морица;
- поэмы-трилогии Яноша Араня «Тольди»;
- сборника стихов Аттилы Йожефа.
Библиотекарь вспомнил следующее:
1) в библиотеку заходили Андриш, Фери, Илонка, Кати и Шаньи;
2) есть строгое правило выдавать только по одной книге, причем новую книгу выдают лишь после того, как возвращена предыдущая;
3) Фери как-то раз брал Диккенса, но давно возвратил, так что взять эту книгу вторично Фери не мог;
4) у Андриша две литературные привязанности-стихи Аттилы Йожефа и романы Жюля Верна (книги других авторов Андриш взять не мог);
5) Кати отдает предпочтение литературе ХХ века;
6) Илонка читает произведения только венгерских авторов;
7) Шаньи – неизменный почитатель поэзии (всей остальной литературы для него просто не существует).
Все ли правильно вспомнил Пишта?
-
После опроса пассажиров четырех маршрутов трамвая: 55, 15, 25 и 33-го, среди которых были Аладар, Петер, Вилмош и Лайош, оказалось по одному представителю четырех профессий: слесарь, электромонтер, маляр и фрезеровщик, выяснилось что:
1) номер трамвайного маршрута, которым следует Вилмош, начинается не с единицы;
2) о 33 маршруте рассказывал кто-то из рабочих-металлистов;
3) номер трамвайного маршрута, которым следовал фрезеровщик, составлен из таких цифр, что их сумма равна числу букв в имени фрезеровщика;
4) Лайош рассказывал о трамвайном маршруте, номер которого состоит из двух одинаковых цифр;
5) Имя электромонтера начинается не с буквы В;
6) Петер спросил у опрашивающего, где лучше сойти, чтобы пересесть на двадцать пятый маршрут;
7) В памяти опрашивающего вдруг отчетливо всплыла фраза, сказанная Лайошем кому-то из пассажиров:»Вы сели не на тот трамвай, вам нужно пересесть на пятьдесят пятый».
Определите имя и профессию каждого пассажира, номер маршрута, о котором он рассказал?
-
Вчера вечером:
1) Андраш отправился на концерт;
2) Бела провела все время с Ольгой;
3) Чаба так и не увиделась с Рози;
4) Панни побывала в кино;
5) Рози посмотрела спектакль в театре
6) Кроме названных постоянными членами той же компании были Дьердь и Шари.
7) Вместе с каждым юношей на том же виде культурных развлечений присутствовала одна девушка.
8) Какая-то пара посетила художественную выставку.
Кто с кем был и где?
-
У каждого из шести людей (обозначим их U, V, W, X, Y b Z) имеется свое увлечение. Один из них собирает насекомых (н), другой – радиолюбитель (р), третий – филателист (ф), четвертый коллекционирует почтовые открытки (о), пятый строит авиамодели (а), шестой – модели электрических железных дорог (жд). Разумеется, увлечения мы перечислили не в том порядке, в котором назвали «имена» людей. Профессии у всех шестерых также различные (их мы назовем также не в том порядке, в котором назвали «имена» людей): электромонтер (э), машинист тепловоза (м), забойщик (з), токарь (т), инженер (и) и врач (в).
Известно о них следующее:
1) U строит модели.
2) Z как то раз пожаловался W, что не разбирается в электротехнике, но W ничем не смог помочь. В радиотехнике он еще кое-как разбирается, а вот заниматься электротехникой ему никогда не приходилось.
3) У X и Y ни профессия, ни «хобби» не имеют ничего общего с железной дорогой.
4) Врач в свободное время с увлечением строит модели.
5) U занимается физическим трудом.
6) X, Y и машинист тепловоза сошлись на том, что они не могли бы насаживать букашек на булавки, хотя дело это, казалось бы, и нехитрое.
7) Профессия человека, который увлекается авиамоделизмом, не начинается с тех букв, которые встречаются в слове «экзамен».
8) Машинист тепловоза и Y всегда отдает филателисту почтовые марки со всех писем, которые они получают.
9) Забойщик не разбирается в радиотехнике. Когда у него испортился радиоприемник, то неисправность устранил энтомолог-любитель.
10) Z дружит с инженером.
11) Любитель строить модели электрических железных дорог занимается умственным трудом.
Определите, у кого какая профессия и кто чем увлекается.
-
Один человек спросил у другого, сколько у того детей и каков их возраст.
- У меня три сына и у всех трех сегодня день рождения. Если перемножить число лет, исполнившихся каждому, то произведение возрастов будет равно 36.
Если сложить те же три числа, то получится число, которое сегодня стоит на календаре. Когда родился младший сын, то два старших отправились сообщить приятную новость бабушке и дедушке, которые живут на другом конце города.
Сколько лет каждому из сыновей и какое число на календаре?
-
Фери, Дьюси, Лаци и Шаньи играли на улице в футбол, как вдруг неудачно посланный мяч попал в окно. От мощного удара стекла разлетелись на мелкие осколки.
Позже выяснилось, что:
Фери.
1) В окно попал не я.
2) Это Шаньи предложил играть в футбол на улице.
3) Лаци не виноват в том, что разбили окно.
Дьюси.
4) Мячом в окно попал не я.
5) Это сделал Лаци.
6) Я умею играть в футбол лучьше, чем Шаньи.
Лаци.
7) Последний удар по мячу нанес не я.
8) Если бы я знал, чем все это кончится, ни за что не стал бы играть в футбол с ребятами.
9) Фери не виноват.
Шаньи.
10) Окно разбил не я.
11) Это сделал Лаци.
12) Когда я пришел, игра была в полном разгаре.
Каждый из ребят дал два правильных и одно ложное показание.
Кто разбил окно?
|
|