Восстановление логической функции по таблице истинности.
СДНФ
Cовершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в которой каждая переменная входит только один раз (возможно с отрицанием)
Пример

СКНФ
Cовершенной конъюктивной нормальной формой (СКНФ) называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно с отрицанием)
Пример
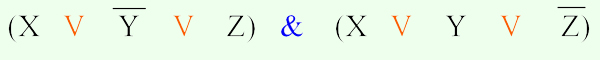
Любую функцию, кроме констант 0 и 1, можно представить в виде как СДНФ, так и СКНФ
Алгоритм получения СДНФ по таблице истинности.
Отметить те строки ТИ, в последнем столбце которых стоят "1":
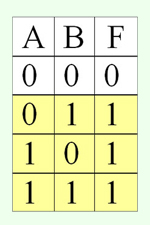
Выписать для каждой отмеченной строки конъюнкцию всех переменных:
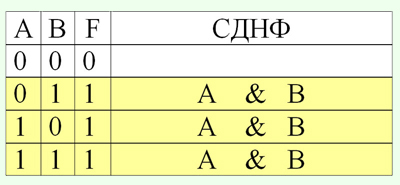
причем, если значение некоторой переменной в данной строке равно "1", то в конъюнкцию включают саму эту переменную, а если значение переменной равно "0", то ее отрицание:
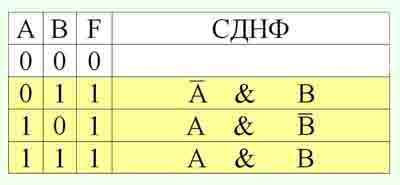
Все полученные конъюнкции связать в дизъюнкцию - составить СДНФ:
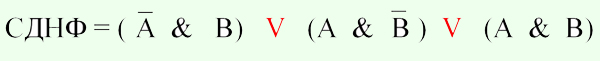
По аналогии определить СКНФ:
В строках ТИ, в последнем столбце которых стоят "0" записать дизъюнкции всех переменных, причем, если значение некоторой переменной в данной строке равно "0", то в дизъюнкцию включают саму эту переменную, а если значение переменной равно "1", то ее отрицание:
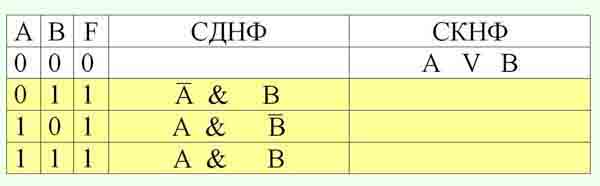
Составим СКНФ:
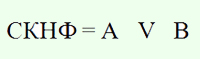
ПРАВИЛО.
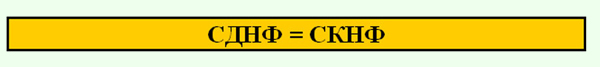
Докажем это равенство, упростив СДНФ:
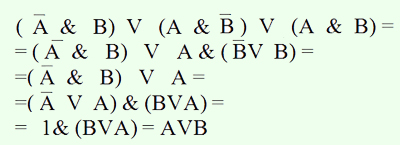
Пример
Дана таблица истинности. Восстановить функцию.
Работа в классе
Восстановить функцию по таблице истинности.
ДОМАШНЕЕ ЗАДАНИЕ
Восстановить функцию по таблице истинности.
|
|