Таблицы истинности логической функции трех переменных.
Для определения истинности составного высказывания по истинности входящих в него элементарных составляют таблицы истинности.
В таблицах "0" обозначают ложное высказывание, а "1" истинное.
Таблицы истинности основных логических функций , были рассмотрены а курсе 8 класса.
Составить таблицу истинности для логической функции:
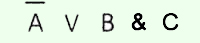
1. Определить порядок действий в соответствии с порядком выполнения логических операций в сложном логическом выражении:
1) инверсия
2) конъюнкция
3) дизъюнкция
4) импликация
5) эквивалентность
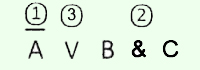
2. Определить размерность таблицы истинности.
"Шапка" таблицы содержит две строки - номера действий и логические операции действий.
Количество столбцов определяется количеством логических переменных (их три А, В, С) и количеством действий (их тоже три).
Количестко строк в таблице равно двойке в степени, равной количеству логических переменных - в случае трех переменных получается 8 строк..
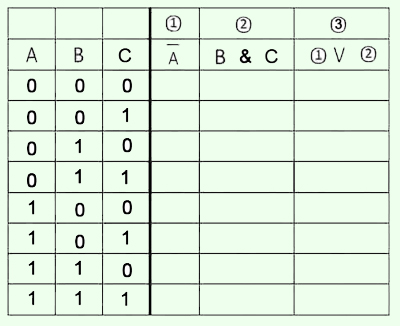
3. Поочередно заполнить столбики таблицы в соответствии с логической функцией данного столбца.
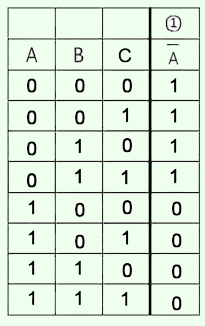
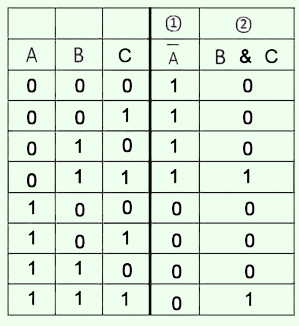
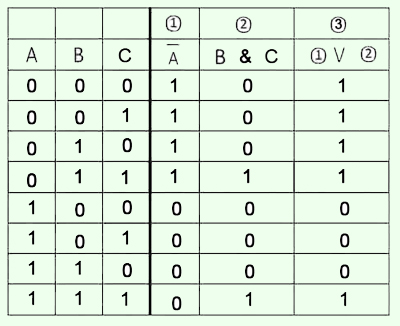
4. Сформулировать ответ.
В последнем столбце "1", соответствует "0" переменной А, а также ситуация, когда все три функции равны "1".
Получается, что данная функция истинна тогда, когда логическая переменная А ложна и когда все три переменные истинны.
ДОМАШНЕЕ ЗАДАНИЕ.
Составить таблицы истинности.

|
|